
Artigo escrito por Henrique Branco • Desenvolvedor RPA na Cellere, com 3 anos de experiência profissional com análise e ciência de dados e automação de processos, incluindo empresas multinacionais (Bosch e ADM do Brasil).
Todos os exemplos neste tutorial foram inspirados no livro Python para análise de dados, do autor Wes Mckinney, desenvolvedor do pacote Pandas. Este livro tem um capítulo inteiro sobre NumPy que serviu de inspiração e motivação para criação do tutorial.

Primeiramente gostaria de compartilhar um pouco do que aprendi com o NumPy, cobrindo desde funções básicas até mais avançadas. Caso você nunca tenha ouvido falar do NumPy antes, fique tranquilo, pois tudo será explicado em detalhes, com códigos comentados, demonstrando o passo a passo!
Neste post você vai aprender os seguintes pontos:
- O que é o NumPy
- Porque o NumPy é tão veloz
- Onde o NumPy é utilizado
- Instalar o Numpy
- Criar arrays com o NumPy
- Tipos de dados do array
- Aritmética com arrays NumPy
- Indexação e fatiamento de arrays
- Transposição e rearranjo dos eixos de arrays
- Funções universais do NumPy
- Expressões lógicas condicionais com arrays
- Métodos para arrays booleanos
- Ordenação de arrays
- Bibliografia utilizada
O que é o NumPy?
NumPy, uma abreviação para Numerical Python, é uma das, se não a principal, biblioteca em Python para computação científica. Ela nos fornece um objeto chamado array multidimensional, que é extremamente veloz para cálculos matemáticos e numéricos.
Porque o NumPy é tão veloz?
NumPy foi escrito (em sua maior parte) em linguagem C, que é uma linguagem de baixo nível, o que torna a biblioteca extremamente veloz, e escondendo toda sua complexidade em um módulo Python simples de utilizar.
Outra diferença é que o NumPy armazena os dados em memória, ao contrário das listas em Python, de modo que as funções possam acessá-los e manipulá-los de maneira muito mais eficiente.

Em contrapartida, tal performance tem um custo. O NumPy, por esta caracterísitca, só trabalha com dados homogêneos (em sua maioria numéricos), ou seja, um array só pode conter um tipo de dado, diferente de uma lista em Python, onde pode-se misturar diversos tipos de dados em uma única lista.
Onde o NumPy é utilizado?
Existem diversas tecnologias na atualidade que se beneficiam da performance do NumPy para cálculos matemáticos.
- Machine Learning: Durante a construção de modelos de Machine Learning, os algoritmos esperam receber os dados em formato numérico, ou em forma de matriz. A biblioteca NumPy é uma das mais utilizadas nas transformações de dados e pré-processamento durante o pipeline de Machine Learning.
- Visão computacional e inteligência artificial: Toda imagem é vista pelo computador como um conjunto de pixels, que são traduzidos para matrizes numéricas de acordo com cores, saturação e outras características das imagens. O NumPy apresenta-se como uma excelente ferramenta para esse tipo de aplicação.
- Estatística: Com o advento do Big Data, a quantidade de dados imensa junto com a aplicabilidade do NumPy para cálculos estatísticos, matemáticos e matriciais tem mostrado todo seu potencial atualmente.
- Engenharias: O NumPy é utilizado em engenharias pois possui funcionalidades interessantes e aplicáveis para a área em questão, como cálculos complexos, transformadas de fourier, derivadas, integrais.
Arrisco a dizer que o NumPy é um concorrente forte, free e open-source da plataforma proprietária MATLAB (https://www.mathworks.com/products/matlab.html), muito utilizada em diversas disciplinas de engenharia. Eu mesmo utilizei (sou engenheiro de formação) durante as aulas de Transferência de Calor (não, não conhecia Python, muito menos NumPy!).
Tem um artigo bastante interessante sobre esse tema (em inglês): https://realpython.com/matlab-vs-python/
Documentação oficial
A documentação oficial do NumPy pode ser encontrada neste link: https://numpy.org/doc/stable/
Atualmente o NumPy está na sua versão 1.19 no dia em que escrevo esse artigo (agosto de 2020)
Instalando o NumPy
O único pré-requisito é ter o Python instalado. A forma mais rápida de instalar o NumPy é via prompt de comando.
pip install numpyO Anaconda é uma das plataforma mais populares para ciência de dados. O pacote NumPy já vem instalado no ambiente base da distribuição do Anaconda, que pode ser baixada através do link https://www.anaconda.com/products/individual

Criando arrays com NumPy
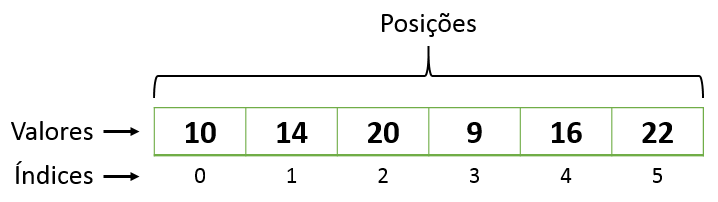
Arrays são o tipo de objeto básico do NumPy. São como listas em Python, que contém valores armazenados em posições.
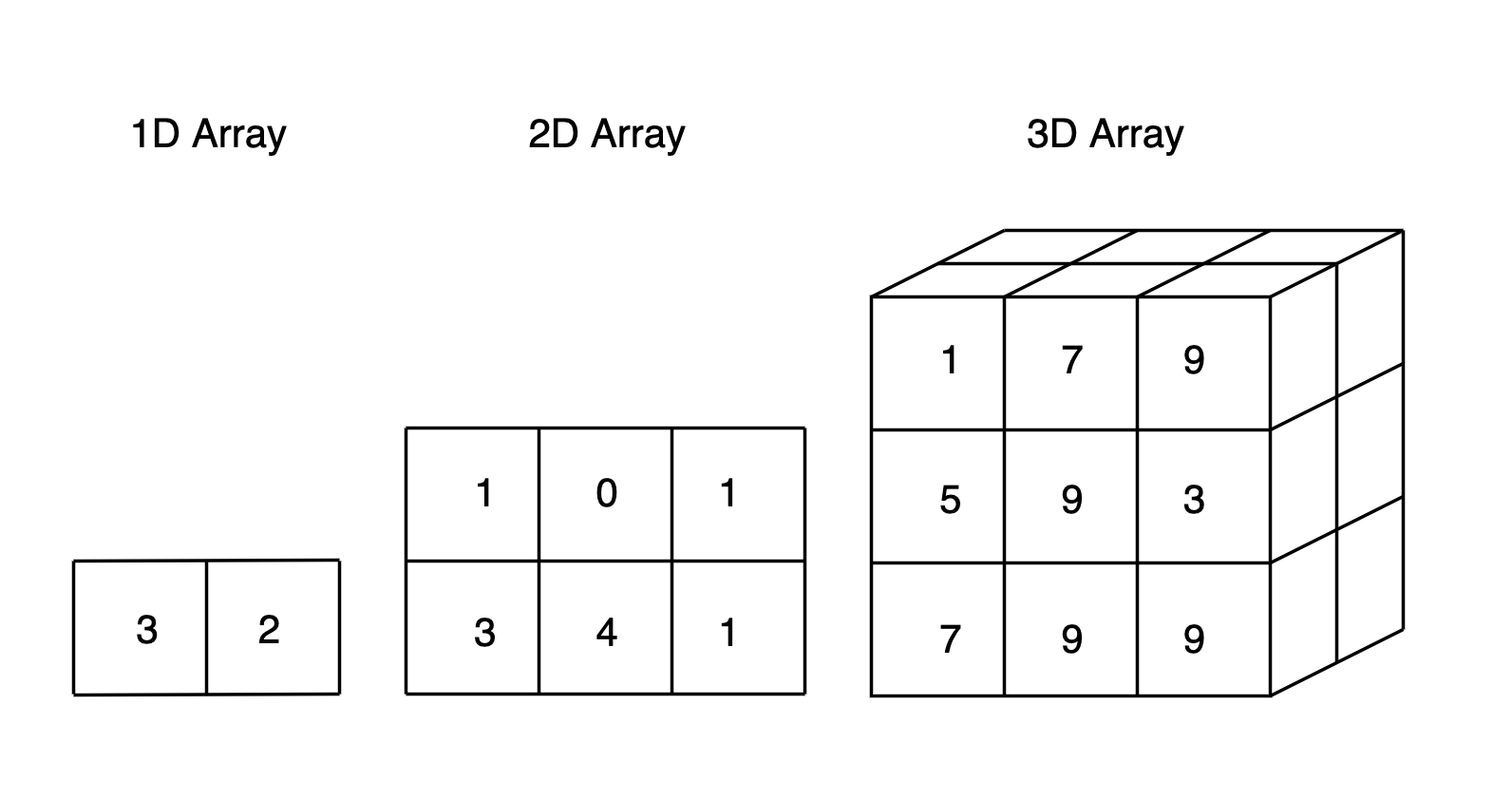
Um array também pode ser multidimensional, não se limitando apenas à 3D, dimensão máxima que o ser humano consegue compreender.
Um array pode ser criado com a função array, que recebe um objeto sequencial (incluindo outros arrays) e gera um novo array NumPy.
>>> import numpy as np
# Criamos uma lista em Python
>>> data = [1, 2, 3, 4, 5, 6]
# Passamos a lista como parâmetro para a função array do NumPy
>>> arr = np.array(data)
# Vamos nos certificar que arr é do tipo array NumPy?
>>> type(arr)
numpy.ndarray
# E finalmente vamos imprimir o conteúdo de arr
>>> arr
array([1, 2, 3, 4, 5, 6])Podemos criar arrays multidimensionais com listas aninhadas.
# Criamos uma lista aninhada
>>> data = [[1, 2, 3], [4, 5, 6]]
# Passamos a lista aninada como parâmetro
>>> arr_2d = np.array(data)
# O tipo de dado continua sendo um array NumPy
>>> type(arr_2d)
numpy.ndarray
# Imprimimos a variável arr_2d
>>> arr_2d
array([[1, 2, 3],
[4, 5, 6]])A partir do array multidimensional acima, podemos começar a explorar alguns de seus atributos.
# O atributo ndim nos fornece o número de dimensões do array
>>> arr_2d.ndim
2
# O atributo shape nos diz quantos elementos temos em cada dimensão
>>> arr_2d.shape
(2, 4)Existem outras formas para se criar arrays especiais com as funções zeros e ones
# Criar um array com todos valores nulos
>>> np.zeros(10)
array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])
# Para criar um array multidimensional de zeros, vamos passar uma tupla como parâmetro
>>>np.zeros((3, 6))
array([[0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0.]])
# Podemos usar o ones para criar um array preenchido com 1
>>>np.ones(4)
array([1., 1., 1., 1.])Para gerar uma sequência, utilizamos o arange, equivalente ao range em Python.
# Vamos gerar agora uma array sequencial com 20 elementos?
>>>np.arange(20)
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19])Percebam que a função arange, assim como o range, inicia sua contagem em 0, e o número inserido como parâmetro não é incluso no array.
Tipo de dados em arrays
O tipo de dado, ou dtype, é uma informação de metadados, ou seja, são dados sobre os dados. Ele nos informa qual é o tipo de dado armazenado em memória.
# Vamos criar um array e informá-lo que desejamos que o dado seja float...
>>>arr1 = np.array([1, 2, 3], dtype = np.float64)
# ... e outro array, onde os mesmos dados serão armazenados como int
>>>arr2 = np.array([1, 2, 3], dtype = np.int32)
# Vamos checar o tipo de dados de ambos os arrays?
>>>arr1.dtype
dtype('float64')
>>>arr2.dtype
dtype('int32')Não é necessário, em hipótese alguma, decorar os tipos de dado, mesmo porque eles estão disponíveis na própria documentação oficial do NumPy neste link: https://numpy.org/devdocs/user/basics.types.html.
Aconselho a ver os outros tipos de dados a título de curiosidade. É bom saber que existe!
A avaliação sobre o tipo de dado também e possíveis alterações serão muito úteis caso o conjunto de dados seja muito grande, casos em que o armazenamento pode gerar problemas de performance.
Alterar o tipo de dado em muitos livros é mencionado como casting.
Podemos também alterar o tipo de dado com o método astype( ).
# Perceba que quando não definimos o tipo de dado...
>>>arr = np.array([1, 2, 3])
# ... o NumPy tenta inferir o tipo, baseado nos valores de entrada
>>>arr.dtype
dtype('int32')
# Podemos alterar o tipo de dado com o método astype()
>>>float_arr = arr.astype(np.float64)
# Que tal conferir se a mudança foi feita?
>>>float_arr.dtype
dtype('float64')Atenção dobrada ao alterar o tipo de dado! Você pode alterar os dados, se não souber o que faz!
# Podemos transformar qualquer tipo de dado, sabendo que...
>>>arr = np.array([1.4, 3.6, -5.1, 9.42, 4.999999])
# ... quando transformamos de float para int...
arr.astype(np.int32)
# ... as casas decimais serão simplesmente ignoradas! E não se trata de arredondamento, e sim
# truncamento! As casa decimais serão ELIMINADAS! Atente-se!
>>>arr.astype(np.int32)
array([ 1, 3, -5, 9, 4])Podemos alterar entre formatos não-numéricos também.
# Vamos criar um array com string que representam números...
>>>numeric_str = np.array(['1', '2', '3', '4'])
# ... e agora transformá-lo para o tipo de dado desejado
>>>numeric_str.astype(float)
array([1., 2., 3., 4.])E se o casting falhar? O NumPy nos informará uma bela mensagem de erro ValueError
# Caso seja impossível alterar o tipo de dado...
>>>numeric_str = np.array(['c', 'a', '3', '4'])
# ... o NumPy nos informará qual o primeiro elemento que falhou!
>>>numeric_str.astype(float)
ValueError: could not convert string to float: 'c'Aritmética com arrays NumPy
Ao realizar operações aritméticas com arrays, não é necessário iterar pelos itens do elemento, como normalmente é feito com Python. Qualquer operação entre arrays de mesmo tamanho faz a operação ser aplicada a todos os elementos. Esse conceito é chamado de vetorização.
# Vamos criar um array para realizar operações com ele
>>>arr = np.array([[1, 2, 3], [4, 5, 6]])
# Exemplos de operações com arrays
>>>arr + arr
array([[ 2, 4, 6],
[ 8, 10, 12]])
>>>arr + 10
array([[11, 12, 13],
[14, 15, 16]])
>>>arr * arr
array([[ 1, 4, 9],
[16, 25, 36]])
>>>1 / arr
array([[1. , 0.5 , 0.33333333],
[0.25 , 0.2 , 0.16666667]])Podemos comparar arrays. A comparação nos retornará arrays booleanos.
# Criando um array para comparação
>>>arr2 = np.array([[4, 1, 7], [6, 2, -5]])
# Comparando arrays de mesmo tamanho
>>>arr2 > arr
array([[ True, False, True],
[ True, False, False]])Indexação e fatiamento
Indexação e fatiamento parece assustador, mas não é! Se você aprender a ler as entrelinhas do que está escrito no código, você se tornará um expert. Basicamente trata-se da seleção de uma parte de um array. Há diversas formas de se realizar essa operação.
A indexação em Python se inicia pelo 0! O primeiro elemento do array tem índice 0. Esse destaque é porque esse fato pode causar confusão e gerar erros.
# Vamos gerar um array para trabalharmos com fatiamento
>>> arr = np.arange(10)
>>> arr
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
# Aqui vamos filtrar apenas o sexto elemento da lista (índice 5)
>>> arr[5]
5
# Aqui vamos fatiar nosso array para nos retornar os elementos de índice 5, 6 e 7 do array. Na sintaxe seguinte, o elemento à direita dos : é exclusivo, ele não entra no filtro!
>>> arr[5:8]
array([5, 6, 7]) # Retorna os elementos de índices 5, 6 e 7. O 8 é exclusivo!
# Quando atribuímos um valor à um fatiamento de array, ele substitui os valores originais, como podemos ver no exemplo abaixo
>>> arr[5:8] = 12
>>> arr
array([ 0, 1, 2, 3, 4, 12, 12, 12, 8, 9])É importante salientar que toda e qualquer alteração feita no array será refletido no original, e não será feito uma cópia dele, como acontece nas listas em Python.
# Vamos pegar uma fatia de arr
>>> arr_slice = arr[5:8]
>>> arr_slice
array([12, 12, 12])
# Agora vamos fazer uma alteração na fatia que coletamos...
>>> arr_slice[1] = 123456
# ... e percebemos que a alteração se reflete no array original.
>>> arr
array([0, 1, 2, 3, 4, 12, 123456, 12, 8, 9])Podemos coletar um array completo com a seguinte sintaxe
# Este comando retorna todos os valores do array
>>> arr[:]Para fazer um fatiamento a partir de um índice específico até o final ou tudo até o índice específico, utilizamos a sintaxe abaixo.
# Aqui selecionamos todos os elementos a partir do índice 2, incluindo o índice 2.
>>> arr[2:]
array([2, 3, 4, 12, 123456, 12, 8, 9])
# Já para selecionarmos tudo até o índice 4, excluindo o índice...
>>> arr[:4]
array([0, 1, 2, 3])Vamos agora para o fatiamento de arrays com mais dimensões.
# Vamos criar um array com 2 dimensões
>>> arr2d = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
>>> arr2d
array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
# Podemos acessar cada dimensão da seguinte forma
>>> arr2d[2]
array([7, 8, 9])
# E cada elemento de cada dimensão utilizando ambas as sintaxes abaixo
>>> arr2d[2][1] # Selecionamos o elemento com índice 2, e desse
8 elemento o sub-elemento com índice 1.
# A sintaxe acima é equivalente a esta abaixo
>>> arr2d[2,1]
8A lógica para fatiamento de arrays com mais de 2 dimensões segue a mesma lógica.
# Criando um array com 3 dimensões
>>> arr3d = np.array([[[1,2,3],[4,5,6]],[[7,8,9],[10,11,12]]])
>>> arr3d
array([[[ 1, 2, 3],
[ 4, 5, 6]],
[[ 7, 8, 9],
[10, 11, 12]]])
# Selecionando o primeiro elemento (índice 0).
>>> arr3d[0]
array([[1, 2, 3],
[4, 5, 6]])
# Selecionando o elemento com índice 1 e o sub-elemento com índice 0.
>>> arr3d[1, 0]
array([7, 8, 9])
# Da mesma forma, selecionamos o elemento final com os seguintes índices
>>> arr3d[1, 0, 2]
9Para facilitar a visualização, observe as imagens abaixo. As dimensões no NumPy também podem ser chamadas de eixos.
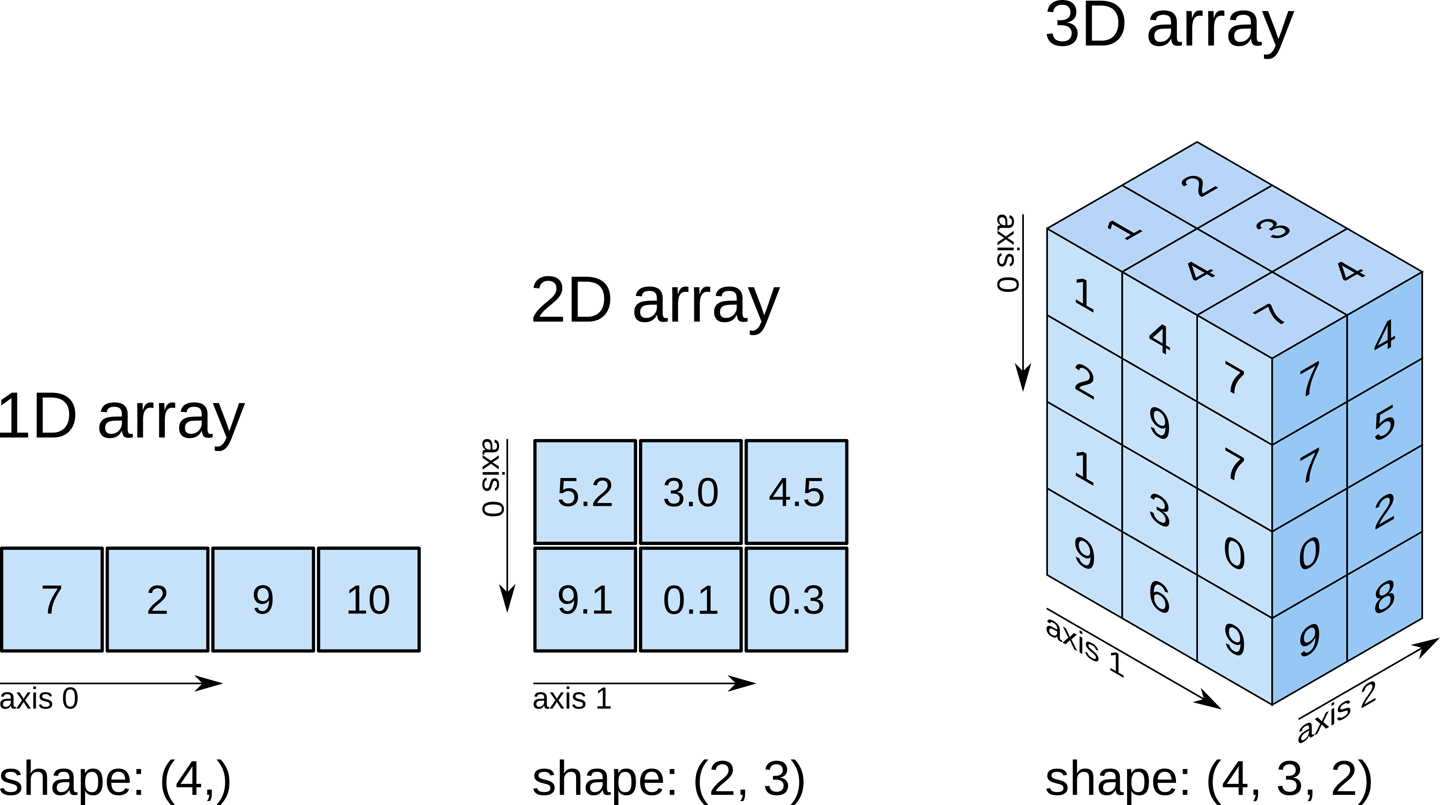
https://fgnt.github.io/python_crashkurs_doc/include/numpy.html

https://www.oreilly.com/library/view/python-for-data/9781491957653/ch04.html
Abaixo mostro uma sintaxe resumida e completa sobre a indexação.
Percebam que os dois-pontos : separam os índices iniciais e finais de uma dimensão ou eixo, enquanto que a , separa as dimensões ou eixos.
arr[indice_inicial_dim0:indice_final_dim0, indice_inicial_dim1:indice_final_dim1, ...]Podemos também utilizar arrays booleanos para filtrar arrays. A partir deste momento, não serão mais comentados as criações de arrays, visto que já deve estar claro para você nesta altura do post.
>>> nomes = np.array(["Maria", "Joaquim", "José", "João", "Bob", "Bob", "Antônio"])
>>> numeros = np.random.randn(7, 4)
>>> nomes
array(['Maria', 'Joaquim', 'José', 'João', 'Bob', 'Bob', 'Antônio'],
dtype='<U7')
>>> numeros
array([[ 0.08332437, 0.74508302, 0.29377823, -0.40309144],
[-0.00657249, -0.37183682, 1.65978568, 0.24354861],
[ 0.92646306, -1.60207788, -0.70337059, 0.04696397],
[ 0.64716676, -0.63640023, -0.83317346, -1.1008962 ],
[ 0.37581831, -1.20021293, 0.73862489, -0.76597305],
[-1.49527206, 0.72298234, 1.59186498, -1.04811938],
[ 0.36767802, -0.43538573, -0.87275053, -0.15102263]])
# Vamos gerar um array booleano de acordo com a condição
>>> nomes == "Joaquim"
array([False, True, False, False, False, False, False])
# Podemos passar o array booleano resultante para filtar outro array. Percebam que somente serão trazidos os resultados cujo array booleano acima for igual a True (segundo elemento, índice 1)
>>> numeros[nomes == "Joaquim"]
array([[-0.00657249, -0.37183682, 1.65978568, 0.24354861]])Podemos inverter um array booleano ou negar uma condição.
# Podemos utilizar o operador != ...
>>> nomes != "Bob"
array([ True, True, True, True, False, False, True])
# ... ou negar a condição com o símbolo ~ . Ambas operações são equivalentes.
>>> ~(nomes == "Bob")
array([ True, True, True, True, False, False, True])Para associarmos várias condições, podemos utilizar os operadores aritméticos booleanos & (E) e | (OU).
# O booleano será True caso o nome seja Maria ou Bob.
>>> condicao_dupla_ou = (nomes == "Maria") | (nomes == "Bob")
>>> dupla_condica_ou
array([ True, False, False, False, True, True, False])Agora, visto que sabemos como trabalhar com operadores booleanos, podemos usar esse conhecimento para atribuir valores diante das condições
# Para substituirmos todos os valores de um array menores que zero por zero
>>>numeros[numeros < 0] = 0
>>> numeros
array([[0.08332437, 0.74508302, 0.29377823, 0. ],
[0. , 0. , 1.65978568, 0.24354861],
[0.92646306, 0. , 0. , 0.04696397],
[0.64716676, 0. , 0. , 0. ],
[0.37581831, 0. , 0.73862489, 0. ],
[0. , 0.72298234, 1.59186498, 0. ],
[0.36767802, 0. , 0. , 0. ]])Pronto. Agora você já é quase um expert em indexação e a partir daqui não falaremos mais no assunto. Vamos apenas utilizar o conhecimento aprendido ao nosso favor ao longo dos próximos tópicos.
Transposição e rearranjo dos eixos de array
Transpor e rearranjar eixos é uma tarefa comum em processamento de dados e cálculos numéricos. Por isso o NumPy fornece uma gama de métodos e funções que facilitam estas atividades.
# Aqui criamos um array sequencial de 0 a 14 (a indexação em Python começa por 0, lembra?)
# e em seguida transformamos esse array para uma matriz com 3 linhas e 5 colunas.
>>> arr = np.arange(15).reshape((3, 5))
>>> arr
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14]])
# Vamos agora calcular a matriz transposta desse array com o atributo .T
>>> arr.T
array([[ 0, 5, 10],
[ 1, 6, 11],
[ 2, 7, 12],
[ 3, 8, 13],
[ 4, 9, 14]])Um cálculo muito comum entre matriz é o produto interno entre matrizes. Podemos utilizar a função np.dot
>>> arr = np.random.randn(6, 3)
>>> arr
array([[ 0.2060784 , 1.13755045, -1.05997268],
[-0.01128338, -1.0281496 , 0.5998368 ],
[-0.42682297, -0.96076494, 0.90979036],
[-1.16368568, 0.23666505, -1.04712259],
[-0.96322389, 0.92656999, 1.00303469],
[-0.36329515, 0.1144878 , 1.25588337]])
# Vamos realizar o produto interno entre a transposta da matriz e ela mesma.
>>> np.dot(arr.T, arr)
array([[ 2.63872147, -0.55338882, -0.81740683],
[-0.55338882, 4.20183165, -1.8712412 ],
[-0.81740683, -1.8712412 , 5.99085209]])Para arrays de dimensões maiores, há outra função chamada transpose que é mais versátil para as transformações.
>>> arr = np.arange(16).reshape((2, 2, 4))
>>> arr
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7]],
[[ 8, 9, 10, 11],
[12, 13, 14, 15]]])
# Aqui vamos rearranjar as linhas, colocando-as na ordem desejada. Aqui trocamos de posição os eixos 0 e 1 do array. O eixo 2 permaneceu no seu lugar.
>>> arr.transpose((1, 0, 2))
array([[[ 0, 1, 2, 3],
[ 8, 9, 10, 11]],
[[ 4, 5, 6, 7],
[12, 13, 14, 15]]])Existe uma forma mais simples para simplesmente trocar eixos de lugar com a função swapaxes, que troca os eixos de lugar para organizar os dados.
>>> arr
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7]],
[[ 8, 9, 10, 11],
[12, 13, 14, 15]]])
# Vamos transpor os eixos 1 e 2 do nosso array.
>>> arr.swapaxes(1, 2)
array([[[ 0, 4],
[ 1, 5],
[ 2, 6],
[ 3, 7]],
[[ 8, 12],
[ 9, 13],
[10, 14],
[11, 15]]])Funções universais do NumPy
Há diversas funções no NumPy. As funções universais recebem esse nome porque são aplicadas a todos os elementos do array, sem a necessidade de usar um loop explícito. Internamente a função faz isso por nós.
# Neste ponto acho que você já sabe como criar um array! =)
>>> arr = np.arange(10)
>>> arr
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
# Função sqrt aplica a raiz quadrada a todos os elementos do array
>>> np.sqrt(arr)
array([0. , 1. , 1.41421356, 1.73205081, 2. ,
2.23606798, 2.44948974, 2.64575131, 2.82842712, 3. ])
# Função exp aplica função exponencial para todos os elementos do array
>>> np.exp(arr)
array([1.00000000e+00, 2.71828183e+00, 7.38905610e+00, 2.00855369e+01,
5.45981500e+01, 1.48413159e+02, 4.03428793e+02, 1.09663316e+03,
2.98095799e+03, 8.10308393e+03])Funções que recebem um único array são chamadas de unárias, há outras que recebem dois arrays e são chamadas de binárias. Apenas a título de curiosidade, informação não muito relevante. Apenas nomenclaturas.
>>> x = np.random.randn(8)
>>> y = np.random.randn(8)
>>> x
array([ 0.13110084, -1.28745148, 0.05075682, 1.49999079, -0.47796974,
-0.05267934, 0.22294321, -1.61524406])
>>> y
array([ 1.84476066, -1.27600921, -0.20664636, 0.53178038, 0.8108552 ,
-0.29695932, -0.72126149, 2.49670696])
# A função maximum calculou o máximo entre os elementos de x e y pa todos os elementos.
>>> np.maximum(x, y)
array([ 1.84476066, -1.27600921, 0.05075682, 1.49999079, 0.8108552 ,
-0.05267934, 0.22294321, 2.49670696])Vou deixar abaixo uma sugestão de outras funções para você pesquisar. Lembre-se: seu aprendizado depende somente de você. Aqui o link da documentação oficial do NumPy com a lista completa de funções universais: https://numpy.org/doc/stable/reference/ufuncs.html
Expressões lógicas condicionais com arrays
O NumPy nos fornece a função np.where que substitui um laço condicional if-else de uso muito comum em programação.
>>> arr = np.random.randn(4, 4)
>>> arr
array([[ 2.65378459, -0.26617645, 1.74227778, -0.57664047],
[ 0.68143909, 1.06673387, 0.88302114, 0.97905302],
[-1.78929889, -0.5908682 , 1.60486155, -0.23343616],
[ 1.54501694, 0.41143977, 0.81735207, -0.41777972]])
# Vamos criar um array booleano para usar como nossa condição
>>> arr > 0
array([[ True, False, True, False],
[ True, True, True, True],
[False, False, True, False],
[ True, True, True, False]])
# Aqui, onde a condição for satisfeita, substituímos o valor por 1, caso não for satisfeita, inserimos -1
>>> np.where(arr > 0, 1, -1)
array([[ 1, -1, 1, -1],
[ 1, 1, 1, 1],
[-1, -1, 1, -1],
[ 1, 1, 1, -1]])
# Neste outro exemplo, vamos substituir os valores positivos por 10 e manter os valores negativos
>>> np.where(arr > 0, 10, arr)
array([[10. , -0.26617645, 10. , -0.57664047],
[10. , 10. , 10. , 10. ],
[-1.78929889, -0.5908682 , 10. , -0.23343616],
[10. , 10. , 10. , -0.41777972]])Métodos matemáticos e estatísticos
Podemos utilizar o NumPy para calcular estatísticas descritivas e agregações, muito comuns em ciência de dados.
>>> arr = np.random.randn(5, 4)
>>> arr
array([[-1.96532817, -1.33723217, -0.01328811, 0.75250257],
[ 0.52911714, 0.46834087, -2.03227292, -2.73062215],
[-1.59003986, -0.28436066, 0.54175223, 0.06031848],
[-0.76166075, -0.58202163, -0.29772519, -1.15139606],
[-1.04267526, 0.5233871 , 1.00418572, -0.60796563]])
# Utilizamos o mean para calcular a média dos elementos do array.
# Ambas as formas são permitidas e trazem o mesmo resultado.
>>> arr.mean()
>>> np.mean(arr)
-0.5258492229122551
# A função sum retorna a soma de todos os elementos do array
>>> arr.sum()
-10.516984458245103Muita das vezes desejamos fazer agregações por linhas ou colunas. Vamos mostrar agora o argumento axis para realizar a troca do eixo no qual o NumPy realiza a operação.
# Aqui estamos calculando as médias para cada coluna...
>>> arr.mean(axis=1)
array([-0.64083647, -0.94135927, -0.31808245, -0.69820091, -0.03076701])
# ... e aqui a soma para cada linha do array.
>>> arr.sum(axis=0)
array([-4.83058691, -1.21188649, -0.79734827, -3.67716279])Podemos também utilizar métodos cumulativos.
>>> arr = np.arange(8)
>>> arr
array([0, 1, 2, 3, 4, 5, 6, 7])
# Geramos um array com a soma cumulativa para cada item no array
>>> arr.cumsum()
array([ 0, 1, 3, 6, 10, 15, 21, 28], dtype=int32)
# Também podemos aplicar essa função para arrays 2d
>>> arr = np.array([[1, 2, 3],[4, 5, 6],[7, 8, 9]])
>>> arr
array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
# Soma cumulativa nas colunas
>>> arr.cumsum(axis=0)
array([[ 1, 2, 3],
[ 5, 7, 9],
[12, 15, 18]], dtype=int32)
# Produto cumulativo nas linhas
>>> arr.cumprod(axis=1)
array([[ 1, 2, 6],
[ 4, 20, 120],
[ 7, 56, 504]], dtype=int32)Recomendo pesquisar sobre estas outras funções matemáticas e estatísticas:
- std, var, min, max, argmin, argmax…
Métodos para arrays booleanos
O NumPy possui 2 métodos bastante úteis para trabalhar com arrays booleanos: any e all.
>>> bool = np.array([False, False, True, False, True])
# O método any retorna True se houver, no mínimo, um True no array
>>> bool.any()
True
# O método all retorna True se todos os elementos do array forem True
>>> bool.all()
FalseOrdenação de arrays
Para ordenar arrays utilizamos o método sort.
>>> arr = np.random.randn(6)
>>> arr
array([-0.92840134, -1.48815739, 1.89720553, 1.09369238, 1.12525732, 0.23375781])
# Ordenando os arrays do menor para o maior
>>> arr.sort()
>>> arr
array([-1.48815739, -0.92840134, 0.23375781, 1.09369238, 1.12525732,
1.89720553])Podemos também ordenar arrays multidimensionais escolhendo um eixo como referência.
>>> arr = np.random.randn(5, 3)
>>> arr
array([[ 0.02125431, 0.77362581, -0.32427196],
[ 0.46589067, 1.2484832 , 0.15474307],
[ 0.07685404, 0.3927895 , 0.87334181],
[ 1.04573832, 0.14331134, 0.64898554],
[ 0.13050785, -0.49445727, -0.21043663]])
# Aqui ordenamos o array nas linhas, do menor para o maior.
>>> arr.sort(1)
>>> arr
array([[-0.32427196, 0.02125431, 0.77362581],
[ 0.15474307, 0.46589067, 1.2484832 ],
[ 0.07685404, 0.3927895 , 0.87334181],
[ 0.14331134, 0.64898554, 1.04573832],
[-0.49445727, -0.21043663, 0.13050785]])Conclusão
A idéia deste post foi passar apenas uma introdução básica ao poderoso NumPy. O post ficou longo, mas acredite, o NumPy contém outras funções complexas, como funções de álgebra linear, e várias outras, que não foram abordadas aqui. Posteriormente pretendo elaborar um post sobre NumPy avançado também.
Muito obrigado por ter valorizado seu tempo lendo até aqui. E meus parabéns, você aprendeu muito sobre o NumPy com este post. Mas ainda há um caminho longo nesta jornada de aprendizado ininterrupto….
Bibliografia utilizada
A grande maioria dos exemplos foram inspirados no livro Python para análise de dados: tratamento de dados com pandas, numpy e ipython do autor Wes McKinney, desenvolvedor do pacote Pandas.
Onde comprar?
Link a para compra do livro no site da Amazon: https://amzn.to/2YcaykH
Participo do Programa de Associados da Amazon, um serviço de intermediação entre a Amazon e os clientes, que remunera a inclusão de links para o site da Amazon e os sites afiliados
Contatos
Gostou desse post? Aprendeu um pouco mais sobre NumPy ? Gostaria de entrar em contato comigo para troca de experiência e discussões posteriores? Clique nos ícones abaixo e me envie uma mensagem!



Seja o primeiro a comentar